给你无向 连通 图中一个节点的引用,请你返回该图的 深拷贝(克隆)。
图中的每个节点都包含它的值 val(int) 和其邻居的列表(list[Node])。
1
2
3
4
| class Node {
public int val;
public List<Node> neighbors;
}
|
测试用例格式:
简单起见,每个节点的值都和它的索引相同。例如,第一个节点值为 1(val = 1),第二个节点值为 2(val = 2),以此类推。该图在测试用例中使用邻接列表表示。
邻接列表 是用于表示有限图的无序列表的集合。每个列表都描述了图中节点的邻居集。
给定节点将始终是图中的第一个节点(值为 1)。你必须将 给定节点的拷贝 作为对克隆图的引用返回。
示例 1:
1
2
3
4
5
6
7
8
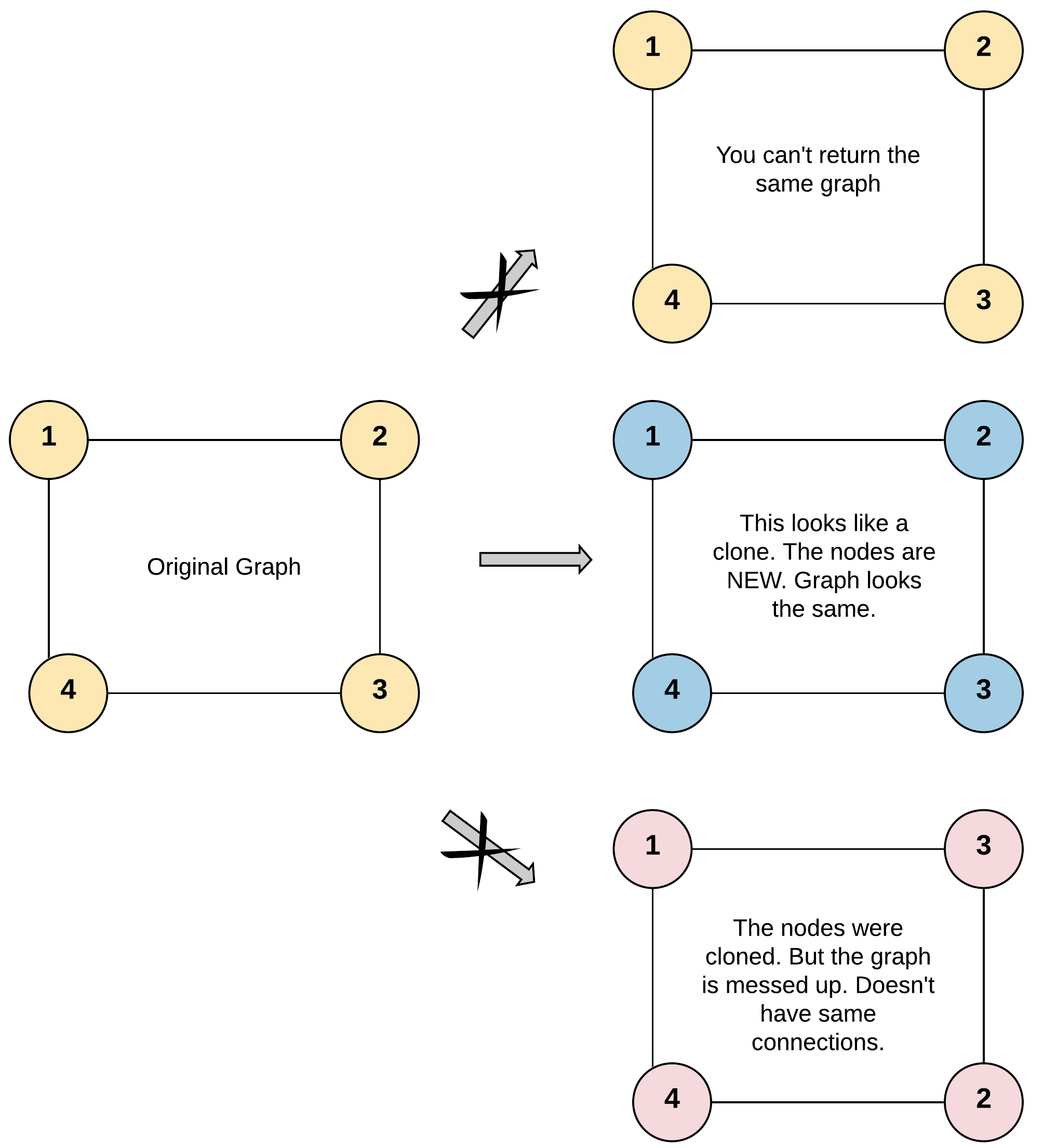
| 输入:adjList = [[2,4],[1,3],[2,4],[1,3]]
输出:[[2,4],[1,3],[2,4],[1,3]]
解释:
图中有 4 个节点。
节点 1 的值是 1,它有两个邻居:节点 2 和 4 。
节点 2 的值是 2,它有两个邻居:节点 1 和 3 。
节点 3 的值是 3,它有两个邻居:节点 2 和 4 。
节点 4 的值是 4,它有两个邻居:节点 1 和 3 。
|
示例 2:
1
2
3
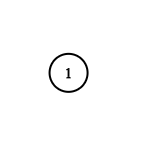
| 输入:adjList = [[]]
输出:[[]]
解释:输入包含一个空列表。该图仅仅只有一个值为 1 的节点,它没有任何邻居。
|
示例 3:
1
2
3
| 输入:adjList =
输出:
解释:这个图是空的,它不含任何节点。
|
示例 4:
1
2
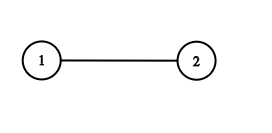
| 输入:adjList = [[2],[1]]
输出:[[2],[1]]
|
提示:
- 节点数不超过 100 。
- 每个节点值
Node.val 都是唯一的,1 <= Node.val <= 100。
- 无向图是一个简单图,这意味着图中没有重复的边,也没有自环。
- 由于图是无向的,如果节点 p 是节点 q 的邻居,那么节点 q 也必须是节点 p 的邻居。
- 图是连通图,你可以从给定节点访问到所有节点。
DFS
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
| class Solution {
public Node cloneGraph(Node node) {
Map<Node, Node> lookup = new HashMap<>();
return dfs(node, lookup);
}
public Node dfs(Node node, Map<Node,Node> lookup){
if(node == null){
return null;
}
if(lookup.containsKey(node)){
return lookup.get(node);
}
Node clone = new Node(node.val);
lookup.put(node, clone);
for(Node n : node.neighbors){
clone.neighbors.add(dfs(n, lookup));
}
return clone;
}
}
|


