冗余连接Ⅱ

685. 冗余连接 II - 力扣（LeetCode）

在本问题中，有根树指满足以下条件的 有向 图。该树只有一个根节点，所有其他节点都是该根节点的后继。该树除了根节点之外的每一个节点都有且只有一个父节点，而根节点没有父节点。

输入一个有向图，该图由一个有着 n 个节点（节点值不重复，从 1 到 n）的树及一条附加的有向边构成。附加的边包含在 1 到 n 中的两个不同顶点间，这条附加的边不属于树中已存在的边。

结果图是一个以边组成的二维数组 edges 。 每个元素是一对 [ui, vi]，用以表示 有向 图中连接顶点 ui 和顶点 vi 的边，其中 ui 是 vi 的一个父节点。

返回一条能删除的边，使得剩下的图是有 n 个节点的有根树。若有多个答案，返回最后出现在给定二维数组的答案。

示例 1：

输入：edges = [[1,2],[1,3],[2,3]]
输出：[2,3]

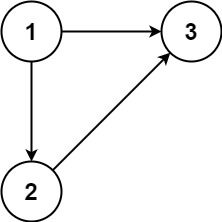
示例 2：

输入：edges = [[1,2],[2,3],[3,4],[4,1],[1,5]]
输出：[4,1]

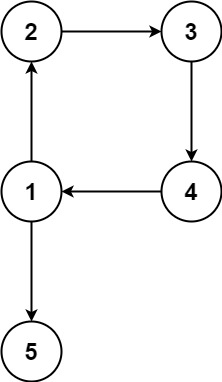
提示：

• n == edges.length
• 3 <= n <= 1000
• edges[i].length == 2
• 1 <= ui, vi <= n

该图由一个有着N个节点 (节点值不重复1, 2, …, N) 的树及一条附加的边构成。附加的边的两个顶点包含在1到N中间，这条附加的边不属于树中已存在的边。

这说明题目中的图原本是是一棵树，只不过在不增加节点的情况下多加了一条边

且该树只有一个根节点，即入度为0的节点只有一个

因为原本就是树，所以增加一条边有可能出现入度为2的顶点，也有可能没有入度为2的顶点（构成有向环）

思路：

情况1和情况2：

先获取入度为2的顶点，将其弧头加入list，有两个弧头（需要倒序遍历），因为答案要求删除后加入的边

如果list不为空，说明有入度为2的顶点

尝试删除其中一条边，删除后不构成有向环，就是要删除的边（删除后会出现有向环的只有情况1），如删除[3,2]，图中存在环，那么必定是删除另一条边[1,2]

情况3：

已经确定图中有环，那么可以直接使用并查集

删除最后一条构成环的边即可

class Solution {

     class UnionFind{
        int[] father;
        public UnionFind(int n) {
            father = new int[n + 1];
            for(int i = 1; i <= n; i++){
                father[i] = i;
            } 
        }

        public int find(int u) {
            if(father[u] == u) return u;
            father[u] = find(father[u]); //路径优化，让u的父节点指向根
            return father[u];
        }

        public boolean isSame(int u, int v) {
            return find(u) == find(v);
        }

        public void join(int u, int v) {
            u = find(u); //找u的父亲
            v = find(v); //找v的父亲
            if(u != v) {
                father[v] = u;
            }
        }
    }


    //判断删除一条边是不是树，使用并查集，如果删除了一条边后出现了环，就不能删除这条边
    public boolean isTreeAfterRemoveEdge(int[][] edges, int deleteEdge){
        UnionFind uf = new UnionFind(edges.length);
        for(int i = 0; i < edges.length; i++){
            if(i == deleteEdge) continue;
            if(uf.isSame(edges[i][0], edges[i][1])){ //删除一条边出现环
                return false;
            }
            uf.join(edges[i][0], edges[i][1]);
        }
        return true;
    }


    int[] inDegree; //记录节点的入度
    
    public int[] findRedundantDirectedConnection(int[][] edges) {
        inDegree = new int[edges.length + 1]; //inDegree[i]为顶点i的入度
        for(int i = 0; i < edges.length; i++){
            inDegree[edges[i][1]] ++; 
        }

        List<Integer> towDegree = new ArrayList<>();
        for(int i = edges.length - 1; i >= 0; i --){ //后加入的度为2的边先加入
            if(inDegree[edges[i][1]] == 2){
                towDegree.add(i); //将使顶点入度为2的弧头加入
            }
        }

        //情况1和情况2，如果有入度为2的点,从两条边中删除一条,看删除哪个之后可以构成树
        if(!towDegree.isEmpty()){
            if(isTreeAfterRemoveEdge(edges, towDegree.get(0))){
                return edges[towDegree.get(0)];
            }else{
                return edges[towDegree.get(1)];
            }
        }


        //没有入度为2的点，一定有环
        UnionFind uf = new UnionFind(edges.length);
        for(int i = 0; i < edges.length; i++){
            if(uf.isSame(edges[i][0], edges[i][1])){ //构成环的最后一条边就是要删除的
                return edges[i];
            }
            uf.join(edges[i][0], edges[i][1]);

        }
        return null;
    }
}