并查集

并查集理论基础

并查集常用来解决连通性问题。

大白话就是当我们需要判断两个元素是否在同一个集合里的时候，我们就要想到用并查集。

并查集主要有两个功能：

• 将两个元素添加到一个集合中。
• 判断两个元素在不在同一个集合

//并查集初始化
public void init(){
    for(int i = 0; i < father.length; i++){
        father[i] = i;
    }
}

//找u的根
public int find(int u){
    if(u == father[u]) return u;
    return find(father[u]); 
}


//判断两个节点是否处于同一个根
public boolean isSame(int u, int v){
    return find(u) == find(v);
}

public void join(int u, int v){
    u = father[u]; //找u的父亲
    v = father[v]; //找v的父亲
    if(u == v) return;
    father[v] = u; //v的父亲指向u的父亲
}

路径压缩

在实现 find 函数的过程中，我们知道，通过递归的方式，不断获取father数组下标对应的数值，最终找到这个集合的根。

如图：

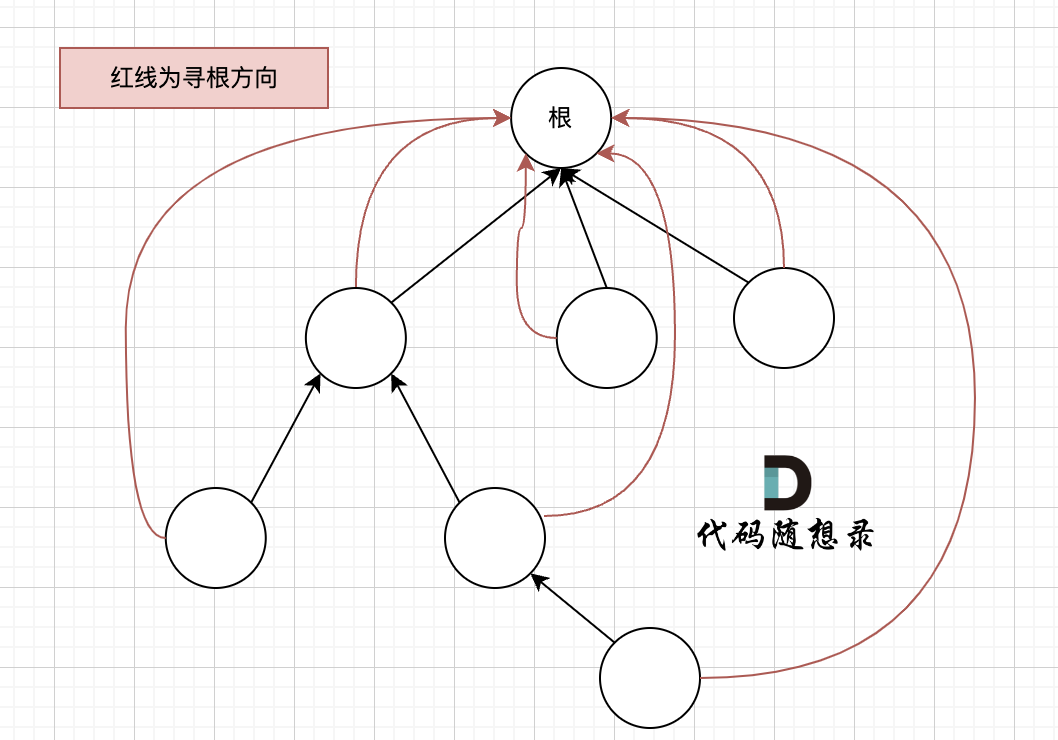
如果这棵多叉树高度很深的话，每次find函数 去寻找跟的过程就要递归很多次。

我们的目的只需要知道这些节点在同一个根下就可以，所以对这棵多叉树的构造只需要这样就可以了，如图：

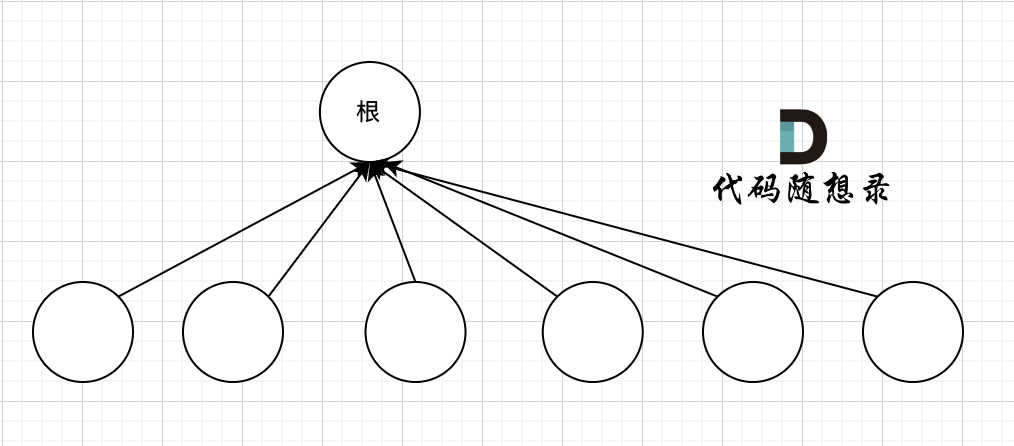
除了根节点其他所有节点都挂载根节点下，这样我们在寻根的时候就很快，只需要一步

我们只需要在递归的过程中，让 father[u] 接住 递归函数 find(father[u]) 的返回结果。

因为 find 函数向上寻找根节点，father[u] 表述 u 的父节点，那么让 father[u] 直接获取 find函数 返回的根节点，这样就让节点 u 的父节点 变成根节点。

//找u的根
public int find(int u){
    if(u == father[u]) return u;
    father[u] = find(father[u]); //路径优化，让u的父节点指向根
    return father[u];
}

public static class UnionFind{
    private int[] father;
    public UnionFind(int n) {
        father = new int[n];
        for(int i = 0; i < n; i++){
            father[i] = i;
        } 
    }

    public int find(int u) {
        if(father[u] == u) return u;
        father[u] = find(father[u]); //路径优化，让u的父节点指向根
        return father[u];
    }

    public boolean isSame(int u, int v) {
        return find(u) == find(v);
    }

    public void join(int u, int v) {
        u = find(u); //找u的父亲
        v = find(v); //找v的父亲
        if(u != v) {
            father[v] = u;
        }
    }
}