太平洋大西洋水流问题

417. 太平洋大西洋水流问题 - 力扣（LeetCode）

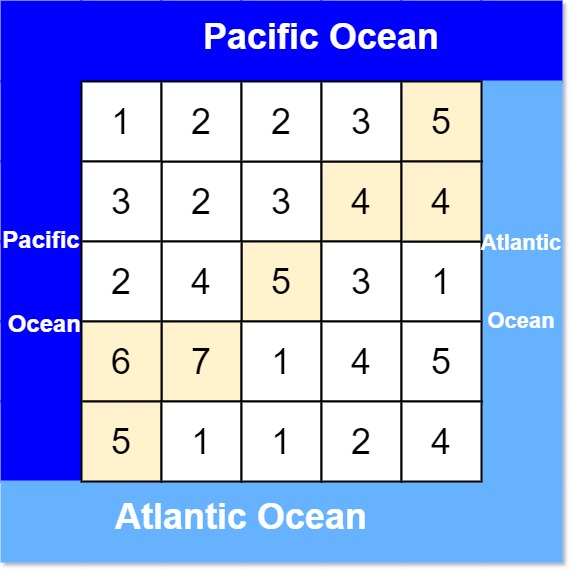
有一个 m × n 的矩形岛屿，与 太平洋 和 大西洋 相邻。 “太平洋” 处于大陆的左边界和上边界，而 “大西洋” 处于大陆的右边界和下边界。

这个岛被分割成一个由若干方形单元格组成的网格。给定一个 m x n 的整数矩阵 heights ， heights[r][c] 表示坐标 (r, c) 上单元格 高于海平面的高度 。

岛上雨水较多，如果相邻单元格的高度 小于或等于 当前单元格的高度，雨水可以直接向北、南、东、西流向相邻单元格。水可以从海洋附近的任何单元格流入海洋。

返回网格坐标 result 的 2D 列表 ，其中 result[i] = [ri, ci] 表示雨水从单元格 (ri, ci) 流动 既可流向太平洋也可流向大西洋 。

示例 1：

img

1
2
输入: heights = [[1,2,2,3,5],[3,2,3,4,4],[2,4,5,3,1],[6,7,1,4,5],[5,1,1,2,4]]
输出: [[0,4],[1,3],[1,4],[2,2],[3,0],[3,1],[4,0]]

示例 2：

1
2
输入: heights = [[2,1],[1,2]]
输出: [[0,0],[0,1],[1,0],[1,1]]

提示：

  • m == heights.length
  • n == heights[r].length
  • 1 <= m, n <= 200
  • 0 <= heights[r][c] <= 105

暴力解法：

遍历每个点，然后看这个点能不能同时到达太平洋和大西洋

使用DFS或BFS遍历要先判断下一个节点是否能到达，在进行遍历

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
class Solution {
    List<List<Integer>> ans = new ArrayList<>();
    List<Integer> pos = new ArrayList<>();
    int[][] move = {{0,1}, {0,-1}, {1,0}, {-1,0}}; 
    boolean[][] visited;
    public List<List<Integer>> pacificAtlantic(int[][] heights) {
        visited = new boolean[heights.length][heights[0].length];


        for(int i = 0; i < heights.length; i++){
            for(int j = 0; j < heights[0].length; j++){
                if(isAns(heights, i, j, visited)){
                    ans.add(List.of(i,j));
                }
            }
        }
        return ans;
    }

    //判断一个节点是否可以同时流向太平洋和大西洋
    public boolean isAns(int[][] heights, int x, int y, boolean[][] visited){

        boolean isPacific = false;
        boolean isAtlantic = false;
        visited = new boolean[heights.length][heights[0].length];

        dfs(heights, x, y, visited);

        //判断是否能到达太平洋
        for(int i = 0; i < heights[0].length; i++){
            if(visited[0][i]) isPacific = true;
        }
        for(int i = 0; i < heights.length; i++){
            if(visited[i][0]) isPacific = true;
        }

        //判断是否能到达大西洋
        for(int i = 0; i < heights[0].length; i++){
            if(visited[heights.length-1][i]) isAtlantic = true;
        }
        for(int i = 0; i < heights.length; i++){
            if(visited[i][heights[0].length-1]) isAtlantic = true; 
        }

        return isPacific && isAtlantic;
    }

    //满足条件再进入dfs
    public void dfs(int[][] heights, int x, int y, boolean[][] visited){
        
        //访问该节点
        visited[x][y] = true;

        for(int i = 0; i < 4; i++){
            int next_x = x + move[i][0];
            int next_y = y + move[i][1];
            if(next_x < 0 || next_y < 0 || next_x >= heights.length || next_y >= heights[0].length || visited[next_x][next_y]){
                continue;
            }
            if(heights[next_x][next_y] <= heights[x][y]){//高度满足条件，可以流向下一个节点
                dfs(heights, next_x, next_y, visited);
            }

        }
    }
}

时间复杂度：$O(m^2 * n^2)$ ：遍历每一个节点，是 m * n，遍历每一个节点的时候，都要做深搜，深搜的时间复杂度是： m * n，这是一个四次方的时间复杂度。

优化：

逆向思维，判断从太平洋或大西洋出发能到达哪些节点
如果一个节点能同时由太平洋或大西洋到达，就是所求的顶点

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
class Solution {
    List<List<Integer>> ans = new ArrayList<>();
    int[][] move = {{0,1}, {0,-1}, {1,0}, {-1,0}}; 
    boolean[][] isPacific;
    boolean[][] isAtlantic;

    public List<List<Integer>> pacificAtlantic(int[][] heights) {
        int n = heights.length;
        int m = heights[0].length;
        isPacific = new boolean[n][m];
        isAtlantic = new boolean[n][m];

        //逆向思维，判断从太平洋或大西洋出发能到达哪些节点
        //如果一个节点能同时由太平洋或大西洋到达，就是所求的顶点
        for(int i = 0; i < m; i++){
            dfs(heights, 0, i, isPacific); //从上边界的太平洋出发
            dfs(heights, n - 1, i, isAtlantic); //从下边界的大西洋出发
        }

        for(int i = 0; i < n; i++){
            dfs(heights, i, 0, isPacific); //从左边界的太平洋出发
            dfs(heights, i, m - 1, isAtlantic); //从右边界的大西洋出发
        }

        for(int i = 0; i < n; i++){
            for(int j = 0; j < m; j++){
                if(isPacific[i][j] && isAtlantic[i][j]){
                    ans.add(List.of(i, j));
                }
            }
        }
        
        return ans;
    }

    //满足条件再进入dfs
    public void dfs(int[][] heights, int x, int y, boolean[][] visited){
        
        //访问该节点
        visited[x][y] = true;

        for(int i = 0; i < 4; i++){
            int next_x = x + move[i][0];
            int next_y = y + move[i][1];
            if(next_x < 0 || next_y < 0 || next_x >= heights.length || next_y >= heights[0].length || visited[next_x][next_y]){
                continue;
            }
            //逆向而流，从低的走向高的
            if(heights[next_x][next_y] >= heights[x][y]){//高度满足条件，可以流向下一个节点
                dfs(heights, next_x, next_y, visited);
            }

        }
    }
}

时间复杂度：$O(2mn)$，因为地图中每个节点最多只会遍历2遍

算法 > 图
#算法
太平洋大西洋水流问题
http://example.com/2023/09/18/算法/图/6. 太平洋大西洋水流问题/
作者
PALE13
发布于
2023年9月18日
许可协议