监控二叉树
968. 监控二叉树 - 力扣(LeetCode)
给定一个二叉树,我们在树的节点上安装摄像头。
节点上的每个摄影头都可以监视其父对象、自身及其直接子对象。
计算监控树的所有节点所需的最小摄像头数量。
示例 1:
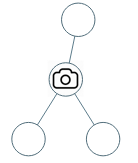
1 | |
示例 2:
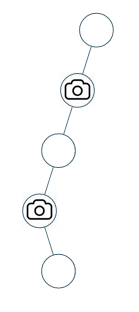
1 | |
提示:
- 给定树的节点数的范围是
[1, 1000]。 - 每个节点的值都是 0。
有如下三种:
- 该节点无覆盖
- 本节点有摄像头
- 本节点有覆盖
我们分别有三个数字来表示:
0:该节点无覆盖
1:本节点有摄像头
2:本节点有覆盖
情况1:左右节点都有覆盖:(left == 2 && right == 2)

- 情况2:左右节点至少有一个无覆盖的情况:(left == 0 || right == 0)
如果是以下情况,则中间节点(父节点)应该放摄像头:
left == 0 && right == 0 左右节点无覆盖
left == 1 && right == 0 左节点有摄像头,右节点无覆盖
left == 0 && right == 1 左节点有无覆盖,右节点摄像头
left == 0 && right == 2 左节点无覆盖,右节点覆盖
left == 2 && right == 0 左节点覆盖,右节点无覆盖
情况3:左右节点至少有一个有摄像头:(left == 1 || right ==1)
如果是以下情况,其实就是 左右孩子节点有一个有摄像头了,那么其父节点就应该是2(覆盖的状态)
- left == 1 && right == 2 左节点有摄像头,右节点有覆盖
- left == 2 && right == 1 左节点有覆盖,右节点有摄像头
- left == 1 && right == 1 左右节点都有摄像头
这个情况2已经判断过了

情况4:头结点没有覆盖
以上都处理完了,递归结束之后,可能头结点还有一个无覆盖的情况

1 | |
监控二叉树
http://example.com/2023/03/05/算法/贪心/18. 监控二叉树/