最长回文子序列

516. 最长回文子序列的长度 - 力扣（LeetCode）

给你一个字符串 s ，找出其中最长的回文子序列，并返回该序列的长度。

子序列定义为：不改变剩余字符顺序的情况下，删除某些字符或者不删除任何字符形成的一个序列。

示例 1：

输入：s = "bbbab"
输出：4
解释：一个可能的最长回文子序列为 "bbbb" 。

示例 2：

输入：s = "cbbd"
输出：2
解释：一个可能的最长回文子序列为 "bb" 。

提示：

• 1 <= s.length <= 1000
• s 仅由小写英文字母组成

动态规划

确定dp数组（dp table）以及下标的含义

dp[i] [j]：字符串s在[i, j]范围内最长的回文子序列的长度为dp[i] [j]。

确定递推公式

在判断回文子串的题目中，关键逻辑就是看s[i]与s[j]是否相同。

如果s[i]与s[j]相同，那么dp[i] [j] = dp[i + 1] [j - 1] + 2;

如图：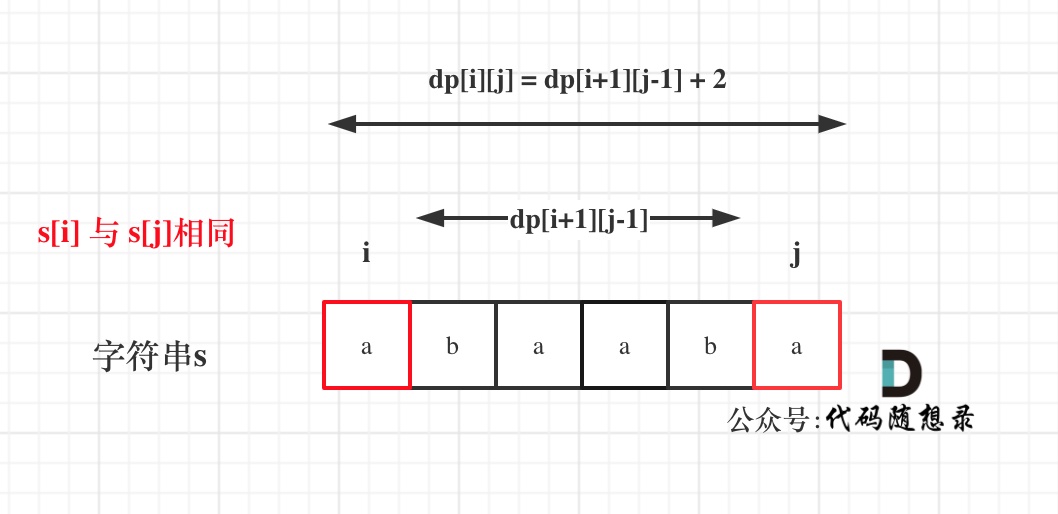

如果s[i]与s[j]不相同，说明s[i]和s[j]的同时加入 并不能增加[i,j]区间回文子序列的长度，那么分别加入s[i]、s[j]看看哪一个可以组成最长的回文子序列。

加入s[j]的回文子序列长度为dp[i + 1] [j]。

加入s[i]的回文子序列长度为dp[i] [j - 1]。

那么dp[i] [j]一定是取最大的，即：dp[i] [j] = max(dp[i + 1] [j], dp[i][j - 1]);

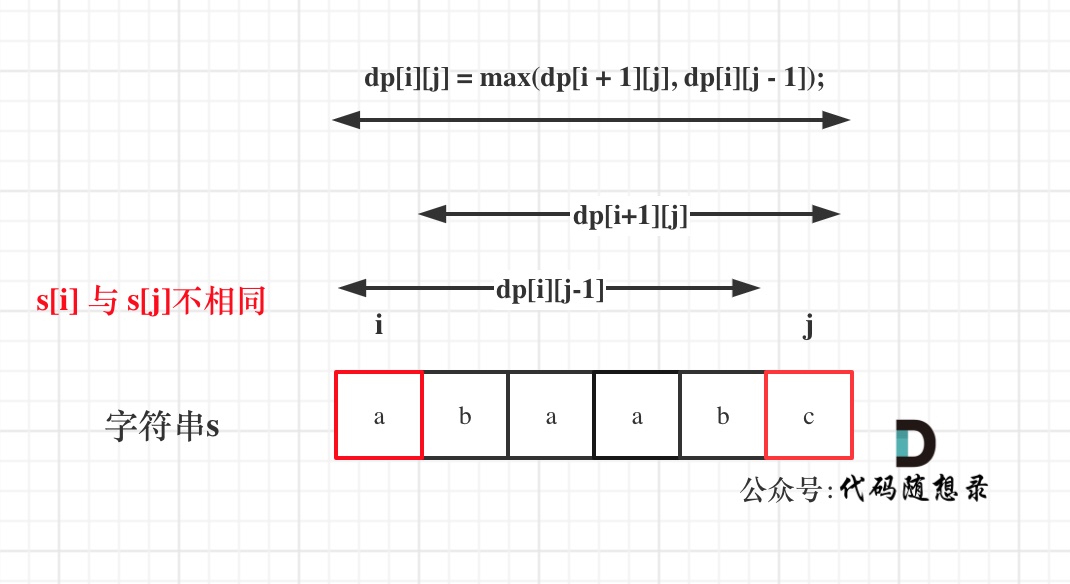
确定遍历顺序

从递归公式中，可以看出，dp[i] [j] 依赖于 dp[i + 1] [j - 1] ，dp[i + 1] [j] 和 dp[i] [j - 1]，如图：

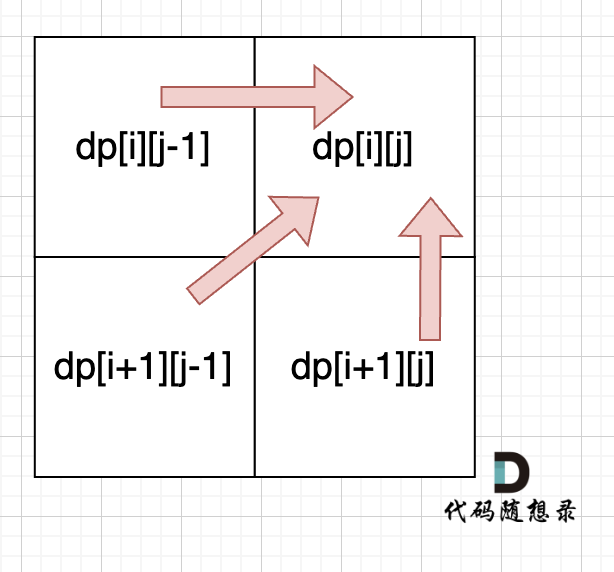
所以遍历i的时候一定要从下到上遍历，这样才能保证下一行的数据是经过计算的。

j的话，可以正常从左向右遍历。

输入s:”cbbd” 为例，dp数组状态如图：

class Solution {
    public int longestPalindromeSubseq(String s) {
        char[] chars = s.toCharArray();
        int len = chars.length;
        int[][] dp = new int[len][len]; //dp[i][j]表示[i,j]中最长回文子序列长度
        
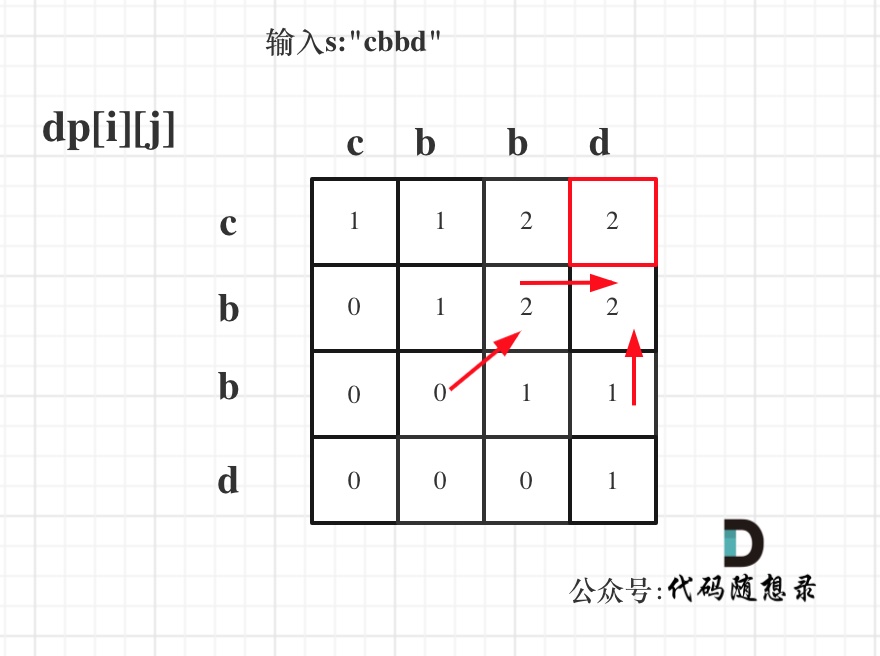
        for(int i = len-1 ; i >= 0; i--){
            for(int j = i ; j < len; j ++){
                if(chars[i] == chars[j]){
                    if(i == j){ //长度为1的或2的且相同一定是回文子串，如a，aa
                        dp[i][j] = 1;
                    }else if(j - i == 1){
                        dp[i][j] = 2;
                    }else{ 
                        dp[i][j] = dp[i+1][j-1]+2;
                    }
                }else{ 
                    dp[i][j] = Math.max(dp[i+1][j], dp[i][j-1]);
                }
                
            }
        }
        return dp[0][len-1];
    }
}