不同的子序列

115. 不同的子序列 - 力扣（LeetCode）

给你两个字符串 s 和 t ，统计并返回在 s 的 子序列 中 t 出现的个数，结果需要对 109 + 7 取模。

示例 1：

输入：s = "rabbbit", t = "rabbit"
输出：3
解释：
如下所示, 有 3 种可以从 s 中得到 "rabbit" 的方案。
rabbbit
rabbbit
rabbbit

示例 2：

输入：s = "babgbag", t = "bag"
输出：5
解释：
如下所示, 有 5 种可以从 s 中得到 "bag" 的方案。 
babgbag
babgbag
babgbag
babgbag
babgbag

提示：

• 1 <= s.length, t.length <= 1000
• s 和 t 由英文字母组成

确定dp数组（dp table）以及下标的含义

dp[i] [j]：以i-1为结尾的s子序列中出现以j-1为结尾的t的个数为dp[i] [j]。

确定递推公式

这一类问题，基本是要分析两种情况

• s[i - 1] 与 t[j - 1]相等
• s[i - 1] 与 t[j - 1] 不相等

当s[i - 1] 与 t[j - 1]相等时，dp[i] [j]可以有两部分组成。

一部分是用s[i - 1]来匹配，那么个数为dp[i - 1] [j - 1]。即不需要考虑当前s子串和t子串的最后一位字母，所以只需要 dp[i-1] [j-1]。即dp[i] [j] = dp[i-1] [j-1]

一部分是不用s[i - 1]来匹配，个数为dp[i - 1] [j]。**即dp[i] [j] = dp[i-1] [j]**，相当于删掉s[i-1]然后匹配

所以当s[i - 1] 与 t[j - 1]相等时，dp[i] [j] = dp[i - 1] [j - 1] + dp[i - 1] [j]。

例如： s：bagg 和 t：bag ，s[3] 和 t[2]是相同的，但是字符串s也可以不用s[3]来匹配，即用s[0]s[1]s[2]组成的bag。

当然也可以用s[3]来匹配，即：s[0]s[1]s[3]组成的bag。

当s[i - 1] 与 t[j - 1]不相等时，dp[i] [j]只有一部分组成，不用s[i - 1]来匹配（就是模拟在s中删除这个元素），即：dp[i - 1] [j]

所以递推公式为：dp[i] [j] = dp[i - 1] [j];

dp数组如何初始化

从递推公式dp[i] [j] = dp[i - 1] [j - 1] + dp[i - 1] [j]; 和 dp[i] [j] = dp[i - 1] [j]; 中可以看出dp[i] [j] 是从上方和左上方推导而来，如图：，那么 dp[i] [0] 和dp[0] [j]是一定要初始化的。

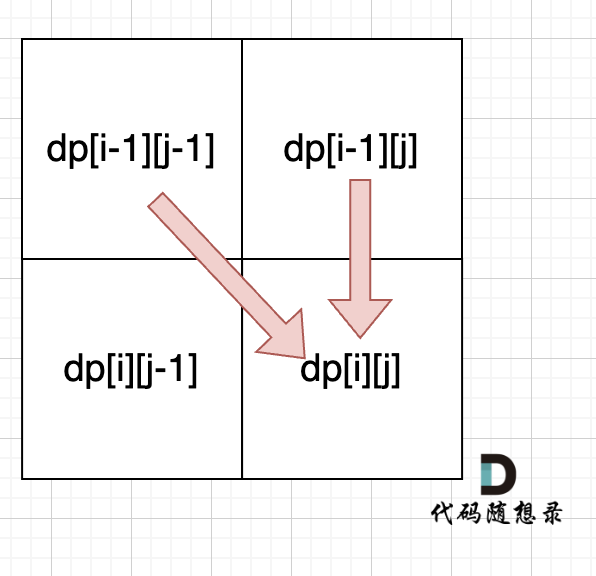
每次当初始化的时候，都要回顾一下dp[i] [j]的定义，不要凭感觉初始化。

dp[i] [0]表示什么呢？

dp[i] [0] 表示：以i-1为结尾的s可以随便删除元素，出现空字符串的个数。

那么dp[i] [0]一定都是1，因为也就是把以i-1为结尾的s，删除所有元素，出现空字符串的个数就是1。

再来看dp[0] [j]，dp[0] [j]：空字符串s可以随便删除元素，出现以j-1为结尾的字符串t的个数。

那么dp[0] [j]一定都是0，s如论如何也变成不了t。

最后就要看一个特殊位置了，即：dp[0] [0] 应该是多少。

dp[0] [0]应该是1，空字符串s，可以删除0个元素，变成空字符串t。

class Solution {
    public int numDistinct(String s, String t) {
        char[] str1 = s.toCharArray();
        char[] str2 = t.toCharArray();
        int len1 = str1.length;
        int len2 = str2.length;
        int[][] dp = new int[len1 + 1][len2 + 1];
        for(int i = 0; i <= len1; i++){ //表示以s以下标i-1为即为出现空字符的数量
            dp[i][0] = 1; //必须初始化为1，否则无法进行迭代计算，因为dp[i][j]依赖于右上元素
        }
        //dp[i][j]表示以下标i-1为结尾的s和以下标j-1为为结尾的t，t在s中出现的次数为dp[i][j]
        for(int i = 1; i <= len1; i++){
            for(int j = 1; j <= len2; j++){ 
                if(str1[i-1] == str2[j-1]){
                    //相等时，可以用s[i-1]来匹配，即dp[i][j] += dp[i-1][j-1]
                    //不用s[i-1]匹配, 即dp[i][j] += dp[i-1][j]
                    dp[i][j] = dp[i-1][j-1] + dp[i-1][j];
                }else{
                    dp[i][j] = dp[i-1][j];
                }
            }
        }
        return dp[len1][len2];
    }
}